IV. Povaha vysvětlení
8.48. Nyní zbývá stručně zrekapitulovat, co by měla teorie nastíněná na předchozích stránkách vlastně objasnit a do jaké míry od ní můžeme očekávat, že bude schopna popsat konkrétní mentální procesy. Je proto nezbytné, abychom přesněji než dosud vymezili, co rozumíme pojmem „vysvětlení“. Tato otázka je zvláště relevantní, neboť „vysvětlení“ je samo o sobě jedním z mentálních procesů, jež má tato teorie za cíl vysvětlit.
8.49. Již dříve bylo naznačeno (5.44-5.48), že vysvětlování spočívá v tom, že se v mozku utváří „model“ komplexu událostí, které mají být vysvětleny; model, jehož části jsou definovány svým postavením v komplexnější struktuře vztahů, jež tvoří polo-permanentní rámec, z něhož jednotlivé reprezentace událostí odvozují svůj význam.
8.50. Tento koncept „modelu“, o němž se má za to, že ho mozek dokáže takto vytvářet, byl samozřejmě v této souvislosti často používán[1] a sám o sobě nás příliš daleko nedovede. Je-li totiž chápán, jak tomu zpravidla bývá, jako samostatný model konkrétního jevu, který má být vysvětlen, není vůbec zřejmé, co se tím vlastně míní. Analogie s mechanickým modelem zde není přímo použitelná. Mechanický model čerpá svůj význam z toho, že se předpokládá, že vlastnosti jeho jednotlivých částí jsou známy a v určitých ohledech odpovídají vlastnostem částí jevu, který je tímto modelem reprodukován. Právě ze znalosti těchto různých vlastností jednotlivých částí odvozujeme naši znalost toho, jak bude daná kombinace těchto částí fungovat.
8.51. Obecně platí, že možnost vytvořit model, který něco vysvětluje, předpokládá, že máme k dispozici jednoznačně vymezené prvky, jejichž působení za různých okolností známe bez ohledu na konkrétní model, v němž je použijeme. V případě mechanického modelu jsou to fyzikální vlastnosti jednotlivých částí, o nichž se má za to, že jsou nám známy. U matematického „modelu“ jsou zase „vlastnosti“ jednotlivých částí definovány funkcemi, které udávají, jakých hodnot budou tyto části nabývat v různých situacích, a které lze kombinovat do různých soustav rovnic, jež tvoří určité modely.
8.52. Slabina běžného používání konceptu modelu jako výkladu procesu vysvětlování spočívá v tom, že tento koncept předpokládá, leč nevysvětluje, existenci různých mentálních entit, z nichž by takový model mohl být vytvořen. Nevysvětluje, v jakém smyslu nebo jakým způsobem části modelu odpovídají částem předlohy ani jaké jsou vlastnosti prvků, z nichž je model sestaven.
8.53. Koncept modelu, který se vytváří v mozku, je užitečný teprve poté, co se nám podaří objasnit různé vlastnosti částí, z nichž je tento model sestaven. Takové objasnění nám poskytuje vysvětlení determinace smyslových (a jiných mentálních) kvalit na základě jejich pozice v komplexnější polo-permanentní struktuře vztahů, „mapě“ světa, kterou v mozku utvářela dosavadní zkušenost a kterou jsme popsali na předchozích stránkách. Je to právě pozice impulzu v propojené síti nervových vláken, která způsobuje, že jeho výskyt spolu s jinými impulzy vyvolá určité další impulzy. Vytváření modelu se tak jeví pouze jako zvláštní případ onoho procesu společné nebo simultánní klasifikace skupiny impulzů, z nichž každý má svůj vlastní význam nezávisle na konkrétní kombinaci či modelu, v němž se právě vyskytuje.
8.54. Tento proces společné klasifikace, který vytváří model, můžeme schematicky znázornit následovně: jednotlivé prvky, tedy mentální kvality, z nichž je model sestaven, jsou třídy impulzů, jež můžeme nazvat A, B, C, atd. a jež jsou definovány tak, že například prvek a (člen A) vyvolá x (a případně i jiné impulzy), pokud se vyskytne ve spojení s o, p,…, ale vyvolá v, z,…, pokud se vyskytne ve spojení s r, s,. . . atd. atd. a podobně pro všechny členy tříd B, C, atd. V této definici se samozřejmě může jakákoli daná třída impulzů vyskytovat jak v „primární“ roli, tj. jako prvek určité třídy definované impulzy, jež vyvolá kterýkoli prvek této třídy, tak i v roli „sekundární“, tj. jako vyvolaný impulz, který určuje třídu, do níž patří některé jiné impulzy. (3.38, 3.55 a násl.). Impulzy třídy A se tak budou vyskytovat nejen ve výrocích typu „jestliže (a, o, p), pak x“ nebo „jestliže (a, r, s), pak (y, z …),“ ale také ve výrocích typu „jestliže (b, c, q), pak (a, t)“ atd.
8.55. Z takovéto determinace různého významu impulzů různých tříd vyplývá, že jakákoli kombinace těchto impulzů vyvolá impulzy, jež představují jiné třídy, a ty zase další, a tak dále, přibližně podle následujícího schematického znázornění:
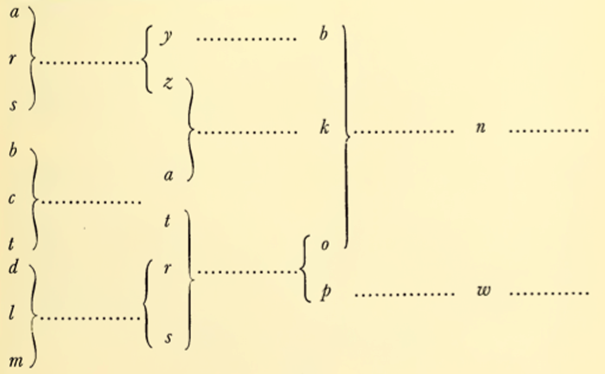
8.56. Konkrétní výsledek je tedy rozpoznán jako důsledek současného výskytu určitých prvků v určité konstelaci, která, kdybychom o jejich přítomnosti věděli, by nám umožnila tento výsledek předpovědět. Jakmile jsme takový model jednou vytvořili, jsme schopni určit, na kterých z různých prvků dané situace pozorovaný výsledek závisí a jak by se změnil, kdyby byl některý z těchto prvků pozměněn – právě to je tím, co nám vysvětlení umožňuje.
[1] Viz zejména K. J. W. Craik, 1943, a K. Lorenz, 1943, str. 343 a 351.
Kniha F. A. Hayeka poprvé vyšla v roce 1952 pod názvem Sensory Order. Na pokračování ji překládá Štěpán Drábek.
Friedrich August von Hayek (8. května 1899 – 23. března 1992) byl rakousko-britský akademik a filosof. Je známý svými příspěvky k politické ekonomii, politické filozofii a intelektuální historii. Hayek se v roce 1974 podělil o Nobelovu pamětní cenu za ekonomii s Gunnarem Myrdalem za práci o penězích a ekonomických výkyvech a vzájemné závislosti ekonomických, sociálních a institucionálních jevů. Jeho popis toho, jak ceny sdělují informace, je široce považován za významný příspěvek k ekonomii, který mu vynesl tuto cenu. Byl významným přispěvatelem rakouské ekonomické školy.
Je autorem mnoha knih, mezi které patří např. Cesta do otroctví; Právo, zákonodárství a svoboda nebo Osudná domýšlivost.








